※本記事は、以前ヤフーブログ「予備校講師採用試験に2回落ちた九大チンカス院生の入試数学語り。」にて2018/2/26に掲載した同名の記事を、ヤフーブログサービス終了に伴い転載したものです。
難易度:標準(飽く迄、「東大としては」)
昨年比:難化
1、微分、目標解答時間10分?
テクニックA
記述量A
発想力B?
総合難易度A
算数ですが、微分した後のsin-sin^3=sin(1-sin^2)に気付かず「よっしゃ2回微分じゃい!」とかするとえらい目に遭います(遭いました(汗)。
自分が時間掛かっといてあれですが、何を問いたい出題なのでしょうか。
2、Cの定義式、連続n整数、互いに素、誘導「結果の利用」、しらみ潰し、目標解答時間25分。
テクニックBC
記述量BC
発想力BC
総合難易度BC
東大はCの定義式好きですね。2015-5とか2009-1とか1999-5とか。
(1)は良いでしょう。n(n+1)は連続2整数の式なので、偶数です。2n+1とn+1が互いに素なのは一言断る必要があると思います。
(2)は(1)の結果の利用です。(1)の結果は、分子はnの1次、分母はnの2次なので、ある程度nが大きくなれば
a(n)<a(n-1)
と分かります。次数による大小感覚は大事です。a(n)は明らかに正なので、「どうせどっかからa(n)<1だろ?」と思ったわけです。つまり、
0<…<a(n+2)<a(n+1)<a(n)<1 で後は全部not整数。
みたいな流れになると予想しました。整数以外が登場する整数問題では、1との大小感覚は常に意識しておく必要があります(cf)京大理系2015-5)。って事で「っしゃやったる!」っつってa(n)を下から順にしらみ潰しに計算したのですが、中々1未満にならない!n=8で漸くそうなりましたが、めっちゃ計算怠かったです。なので、多分模範解答ではないです(汗。恐らく2015-5同様、因数2に注目したりすればもっと綺麗だと思います。
3、軌跡、通過領域、パズル、目標解答時間40分。
テクニックC
記述量CD→BC
発想力C
総合難易度C
2変数の通過領域です。1文字を固定し先ず軌跡を考えるのが第一の選択肢でしょうか。qを固定すると、1変数q混入の放物線の通過領域に落ちます。通過領域の解法は、
(イ)順像法。
(ロ)逆像法。
(ハ)ベクトルの存在領域。
(ニ)素朴に動かす。
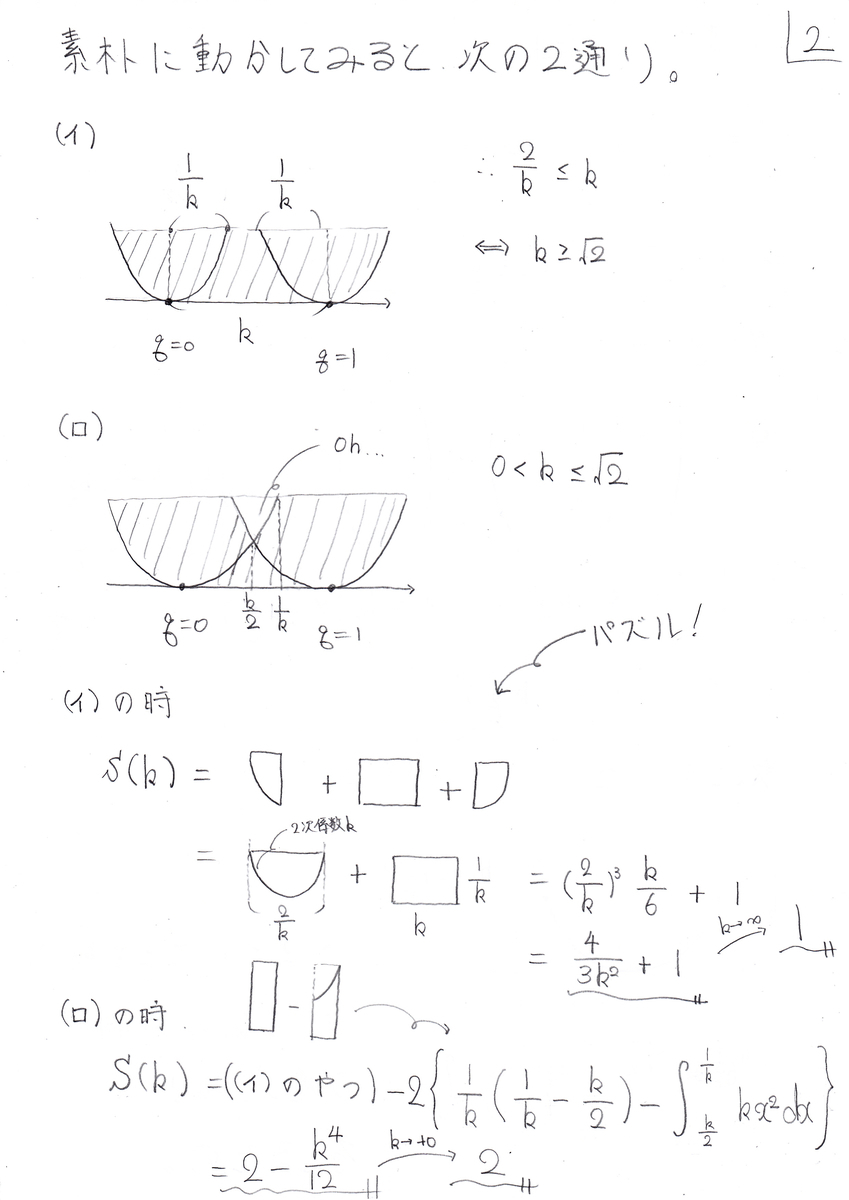
辺りだと思います。本問は、形的に(ハ)を先ず疑いますし、もう少し進んでも(イ)(ロ)辺りに見えるのですが、何と(ニ)です。やられました。去年の5もそうですが、素朴に絵で考える事も大切ですね。
おまけの極限計算2つは、何かのブームなんでしょうか(笑
方針を誤り易く、後半の面積計算も地味に怠いし、そもそもテーマ自体が難しいので、中々の難易度だと思います。解答付けます。

4、解↔交点の言換、不等式(グラフの利用)、目標解答時間10分。
テクニックAB
記述量A
発想力AB
総合難易度AB
これは1同様、ほぼ算数ですが、βと1の大小を、グラフを利用しf(β)とf(1)の大小に言換えるのは要注意です。例によって自分は詰まりました(汗
5、複素数平面総合、軌跡、目標解答時間40分。
テクニックC
記述量CD
発想力C
総合難易度C
もー本当、「取り敢えず対称移動だ分数取るだしまくっときゃ難しくなるだろw」みたいな出題です。学習効果は高いのですが…
(1)は兎に角、複素平面での図形の性質の言換えと複素数の計算です。計算は|z|=1を常に意識しておく必要があります。
(2)は複素平面での軌跡です。方針としては、
(イ)複素平面で押し切る。
(ロ)適当な段階でパラメータを取って図形と方程式に帰着。
(ハ)二次曲線かも。
(ニ)素朴に動かす。
辺りで、(イ)が1番スマートで本問も多分これで出来るのだと思いますが、自分は(ロ)に逃げてしまいました。ただ、こっちの方が着実に解ける場合が多い気もするので、その解答を載せておきます。


※解答は考えるのが面倒だったんでx軸とy軸をひっくり返しています。
6、三次元求積、誘導「結果の利用」、集合、目標解答時間40分。
テクニックBC
記述量CD
発想力C
総合難易度C
これも重い!
(1)(2)は丁寧に考えるだけですが、自分みたいな空間把握能力が低い人間は特に慎重に議論する必要があり、時間が掛かります。
(3)ですが、(2)が大切な誘導です。領域を集合で考えて、普通なら、
V=V1∪V2∪V3-[{(V1∩V2)∪(V2∩V3)∪(V3∩V1)}-V1∩V2∩V3]
なのですが、(2)からV1∩V3⊂V2なので、
V1∩V2∩V3=V1∩V3
となります。こうやって集合で考えるって発想自体が、受験生には馴染みが無くて難しいと思います。
(4)はおまけですね。記述量はあれですけど…
1や4の様な東大らしからぬ易問が有るのは昨年同様ですが、他の問題が去年よりも明らかに難しく、残りの4題は2010年前後の水準だと思います。理系でも1,4以外は計1問分しか解けなかった、みたいな合格者続出なんじゃないでしょうか。暫く易しい路線が続きそうと思っていたので、面食らいました。
ただ、明らかな難問、って感じのやつは居ないので、ちゃんと勉強すれば満点近くも狙えると思います。偉そうな事を言っていますが、自分は今年は3,5は時間内に計算が終りませんでした(汗
後、傾向として特に今年は、領域とか軌跡系の問題が非常に多かった気がします(3~6が全てこのテーマ)。マスターしようとなると、高校数学では軽視されがちな論理、集合をしっかり理解しておく必要があると思うので、個人的には高校数学で1番難しいテーマだと思っています。ですので、特に東大受験生はこの辺りの問題をしっかりと答案を書ける様にすると良いと思います。頻繁に話題にしますが、「入試数学の掌握」の2巻の通過領域がめっちゃ良いです。
※おお!確率が無いっす!ブログを書いている時には全く気付きませんでした。「何が新課程で統計だふざけんなっ!」って事でしょうか?笑