※本記事は、以前ヤフーブログ「予備校講師採用試験に2回落ちた九大チンカス院生の入試数学語り。」にて2017/3/2に掲載した同名の記事を、ヤフーブログサービス終了に伴い転載したものです。
難易度:難
昨年比:難化
1、約数、ディオファントス方程式(積の形)、しらみ潰し、目標解答時間25分。
テクニックB
計算量B
発想力B
総合難易度B
昨年、一昨年に引き続き約数に関する整数問題です。条件から考えられる形を絞り込み、ディオファントス方程式に持ち込みますが、範囲が既に大きく絞られていて、使われるテクニックの数に比して計算が膨らまないのが非常に好印象です。なので解答を載せておきます。
整数の素因数分解表示からの約数に関して考察させる問題は今年で3年連続ですし、東工大志望者は整数問題の特にこれらのトピックが絡む問題を集中的に対策しておくのも良いかもしれません。
昨年の最難問に匹敵し、しかも同一トピックの問題ですが、まさか本問が本セット最易問であるとは…


2、最大値最小値(微分)、絶対値、三角函数の周期性、微積分学の基本定理(の拡張)、三角函数の置換積分、目標解答時間35分。
テクニックBC
計算量C
発想力B
総合難易度BC
数Ⅲのテクニックが1問にこれでもかと詰め込まれ、それでいて行き当たりばったりではない超良問です。来年度以降の各予備校の難関大理系クラスのテキストに引っ張りだこにされる事でしょう(笑
一言だけ、微積分学の基本定理は絶対値を付けたままでも適用出来ます。ただ、いつ外しても処理量は大して変わらないと思いますが。
正しく東工大の微積です。計算量がしょっぱいですが、是非とも完答したい。
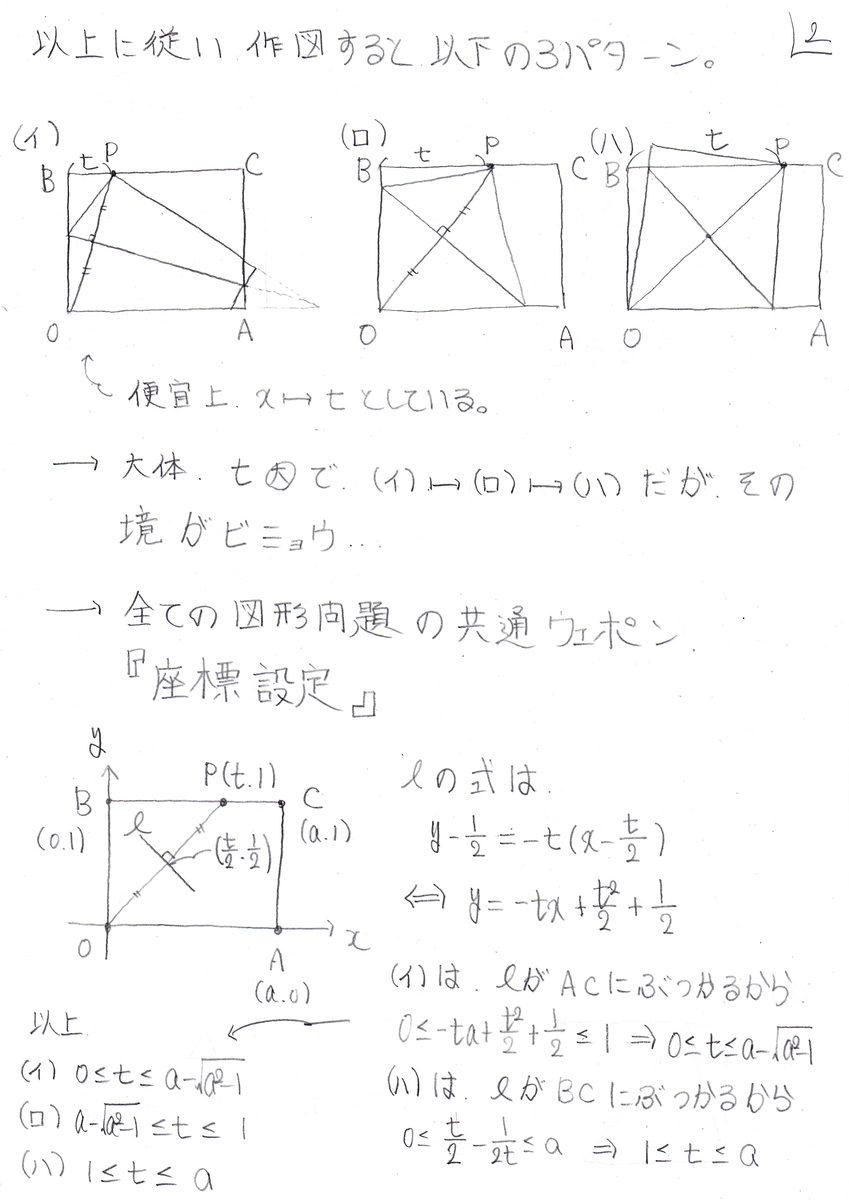
3、作図(折り返し)、座標設定、最大値最小値(微分)、目標解答時間35分。
テクニックBC
計算量C
発想力C
総合難易度C
既にツイッター等でちょっとした話題に上がっている、折り紙問題です。これについては、問題文にそうと書かれていなくても、何なら問題用紙を切り取ってでも実行して欲しいですね。全ての問題を解く上で最も大事な事の1つ、実験です。但しその上で本問程度の作図は、そんな事をしなくても理屈で図示出来る様になって欲しいです。
と言う事で(1)ですが、詳しくは補足をご覧頂くとして、その中の「折り返しを垂線で考える」について一言。これ、実は僕が勝手に考えただけなのですが、2015東北大5(3)と云う前例も在りますし、1つの標語にして構わないと思います。ひょっとしたら中学受験の図形問題なんかでは常識だったりするのかも知れません。補足の所迄出来れば、後は相似やら比やら使うだけですね。
(2)は(1)が出来ればサービス問題で、微分するだけです。計算は中々面倒ですが(汗
さて、東工大では時々、この手の“動的な”図形的考察を必要とされる問題が出題されます。先程も述べましたが、こう云うものは中学受験、或いは高校受験用の本の図形問題のパートなんかに目を通して見ると、ヒントを得られるかも知れません。

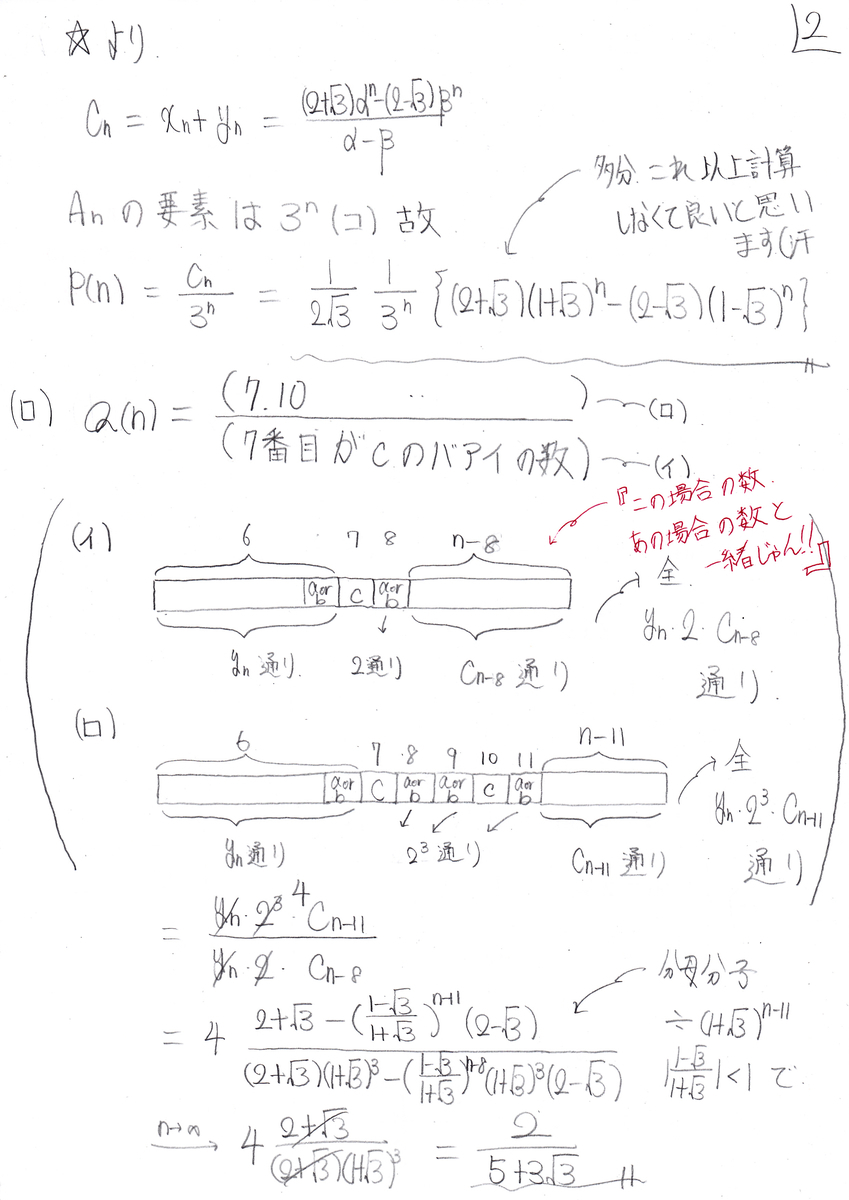
4、確率(条件付きも)、場合の数漸化式(最後の一手で場合分け、連立漸化式、3項間漸化式)、誘導(結果の利用)、目標解答時間35分。
テクニックBC
計算量C
発想力C
総合難易度C
確率ですが、(場合の数)/(場合の数)と考え場合の数を丁寧に求めていきます。
と云う事で(1)は分子を求めなければならないのですが、解答を見て頂ければ分かる通り、漸化式の立式迄に最後の一手で場合分けを2回行っています。立式後の漸化式には√3が絡むので、これらの塊は取り敢えず文字で置いて処理するのが記述量的にベターだと思いますが、受験生は案外苦手なのかも知れません。
(2)は条件付き確率でベイズの定理の利用ですが、これも(確率)/(確率)の分母分子の分母(通じると思います(汗))が各々等しいので、(場合の数)/(場合の数)と見ます。そこでこの場合の数を求めるのに(1)の結果を用いるのですが、結果と言ってもP(n)ではなく、解答中で言うところのCnの方です。結果の利用の中でも若干高級な、「答案の途中の結果を用いる」パターンです。更にこれも直ぐに利用可能な訳ではなく、確率や場合の数によくある、「ここの場合の数(or確率)、よく考えればあの場合の数(or確率)と等しいよね。」ってパターンのやつです(詳しくは解答をご覧下さい)。
標準的なテクニックが複数組み合わされ、そしてその幾つかは適用所で思考力を問われ、更に処理量自体も多い。東工大らしい、重厚な良問です。

5、二次方程式、必要→十分性のチェック、共役解、特称命題(具体的に見つける)、解と係数、一次連立不等式の処理、領域図示(順像法)、二次函数の最大値最小値、目標解答時間40分。
テクニックCD
計算量C
発想力BC
総合難易度C
(1)は必要十分条件の決定です。お約束的な手法として「必要性から絞る→十分性のチェック」が在ります。他に同値変形を繰り返すってのも在って、こちらの方が楽なのですが、本問は解の公式を使って前者でしょう。
(2)は特称命題、つまり存在を示す問題です。手法としては大きく、
①存在に関する定理(中間値の定理等)を用い間接的に示す。
②具体的に1つ見つけてしまう。
の孰れかですが、本問は解と係数の関係から後者でしょう。多項式が絡む問題に於いて、解と係数は常に頭の片隅に置いておくべき事項に1つです。その際、「実係数方程式の複素数解は、その共役も解になる。」を用います。
(3)ですが、(2)の解と係数の関係からa,bがそれぞれc1,c2を用いて表されますので、(1)よりc1,c2とも範囲指定が生じる事から絞込みの必要が生じます。解答中ではc1,c2は各々X,Yとしていますが、この記号で、Yを消去し、bをa,Xの式としますが、この式をaではなくXの式と見て、Xに関する範囲を求めます。所謂「順像法」ってやつですね。詳しくは「入試数学の掌握2」や、大学への数学の“自然流”の説明をご覧下さい。Xに関して二次式なので二次函数の処理になるのですが、場合分けが中々にしょっぱいです。
大取に相応しい、複素数も絡んだ二次式のテクニック詰め合わせ的な問題です。難問と迄はいきませんが、中々の大物だと思います。



では全体概評ですが、今年は難しかった!近年では割と高度だった一昨年も上回り、試験時間延長前、2010年前後の水準です。恐らくは去年の大幅易化で受験生にボコボコにされた反動でしょう。今年は(今年も?)東大京大がとっても大人しかったので、個人的には解いていて凄く楽しかったです(なので解答も沢山です(笑))。やっと僕が思うところの“東工大らしさ”が戻って来た感じでしょうか。
無駄話はこれ位にして基準についてですが、先ず取れそうなのは1と2でしょう。ただ、1は記述漏れや72の消し忘れが怖いですし、2も計算量が大概なので、大体これらを7,8割方、って感じでしょうか。後半3問は孰れも中々に手強いですが、ここから何とか1問分以上集め、1,5+1ちょい=2,5問ちょい分、つまり半分強も取れれば十分だと思います。
ただ、今年の様な東工大らしい東工大の問題って、時々頭の良さも必要としつつも、基本的には標準的なテクニックを1つずつ積み重ねれば解ける問題なんですよね。その意味では、本当に丁寧にテクニックの整理を行った人間なら、満点も十分に狙えると思うのです。今年のセットを時間内に全て合わせる事が出来れば、取り敢えず受験生としては数学は合格レベルです。